Click for SiteMap
Table of Contents
Fluid Dynamics Drag
Initial Thought
Have any of you cycled against 40mph headwind? Is it even possible? If 90% of resistance to moving forward at this speed, is wind resistance, then you would have to be able to average ~36mph in still air, to be able to make forward progress. I have cycled through a tropical storm, where I was moving very, very slowly, and there was water lapping the bottom bracket. What would it take to not be able to make forward progress at all? The following youtube video is an example of just that:
The Dilemma
Equations for drag and power, where (v) is the speed of the object relative to the fluid. Notice the “relative” bit. That means, that land speed is irrelevant for this equation. Even if you stood still, bulk fluid flow is being converted into a form less capable of doing work, increasing the amount of entropy. See https://en.wikipedia.org/wiki/Dissipation. For simplification, let's say that all of the work produced by the cyclist is fully converted into entropy of the fluid (as a mind exercise), then:
Power from cyclist = Rate of production of Entropy
Power from cyclist = Drag Force x (v) = a_constant x (v)^3
Or you can say that you have a Perfect Fluid, where:
Power from cyclist = Rate of decreasing momentum of the fluid
Aside from spokes spinning into the wind, I don't see a difference in drag between a 20mph direct headwind, and rider moving through still air at 20mph. However, the equations from http://www.kreuzotter.de/english/espeed.htm disagrees with this belief. His equation is below in this article.
The equation I am challenging, used drag force multiplied by the velocity of the rider relative to the ground, to calculate power production. After all, F x V gives the units for power. The power produced by the cyclist can also be expressed (and measured), as torque multiplied by angular velocity, or P = T ?. However, if the cyclist comes to a stop, where the forward force from the cyclist is equal to the drag force, then according to this equation, the cyclist is no longer doing work! Which is true, because that's what I was taught. I just don't find it very useful for this particular situation. The fluid is undergoing a rate of change of momentum, despite the complete lack of forward progress from the cyclist. In this case, how do you set up an equation, for the conservation of energy? I believe the correct way to do this, is to calculate the power required to overcome drag as the one above, rather than saying drag power is relative to the forward progress of the cyclist.
Speed & Power Calculations from another site, that I am challenging
The following equations take into account all of the relevant resistance components: Rolling friction including the dynamic (speed-dependent) rolling friction, air drag including the influence of wind speed, mechanical losses, and uphill/downhill forces.
| P | Rider's power |
| V | Velocity of the bicycle |
| W | Wind speed |
| Hnn | Height above sea level (influences air density) |
| T | Air temperature, in ° Kelvin (influences air density) |
| grade | Inclination (grade) of road, in percent |
| ß | (“beta”) Inclination angle, = arctan(grade/100) |
| mbike | Mass of the bicycle (influences rolling friction, slope pulling force, and normal force) |
| mrider | Mass of the rider (influences rolling friction, slope pulling force, and the rider's frontal area via body volume) |
| Cd | Air drag coefficient |
| A | Total frontal area (bicycle + rider) |
| Cr | Rolling resistance coefficient |
| CrV | Coefficient for velocity-dependent dynamic rolling resistance, here approximated with 0.1 |
| CrVn | Coefficient for the dynamic rolling resistance, normalized to road inclination; CrVn = CrV*cos(ß) |
| Cm | Coefficient for power transmission losses and losses due to tire slippage (the latter can be heard while pedaling powerfully at low speeds) |
| ? | (“rho”) Air density |
| ?0 | Air density on sea level at 0° Celsius (32°F) |
| p0 | Air pressure on sea level at 0° Celsius (32°F) |
| g | Gravitational acceleration |
| Frg | Rolling friction (normalized on inclined plane) plus slope pulling force on inclined plane |
Air density via barometric formula:

Rolling friction plus slope pulling force:
![]()
Speed:
In order to solve this Power equation for Velocity V, we write it in the implicit form

so we can use the cardanic formulae to obtain the solutions:
If a2 + b3 = 0:

If a2 + b3 < 0 (casus irreducibilis; in case of sufficient downhill slope or tailwind speed):


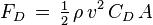


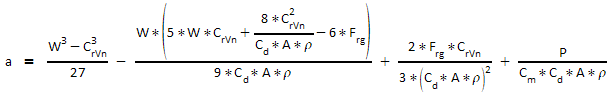
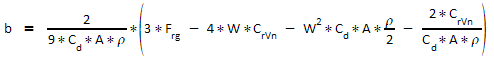

Discussion